একটি মহাকাশযান ও ভেক্টর রাশি বৃত্তান্ত

কো-অর্ডিনেট সিস্টেম

মনেকরো তোমার নাম কাটুশ, তুমি একজন মহাকাশচারী। মহাকাশযানে চেপে একগ্রহ থেকে আরেকগ্রহে ভুসভুস করে উড়ে বেড়াও। একদিন পৃথিবী থেকে কাজটাজ শেষ করে ব্যাগ-ট্যাগ গুছিয়ে মঙ্গলগ্রহের দিকে রওনা দিলে। এবং সুন্দরভাবে মহাকাশযানটি চালিয়ে এদিক ওদিক করে করে গ্রহানুপুঞ্জ এড়িয়ে একসময় মঙ্গলগ্রহে গিয়ে পৌছালে। পৃথিবী থেকে মঙ্গলগ্রহ পর্যন্ত পুরো পথে কখন কতটুকু গিয়ে কত ডিগ্রি কোণে বাঁক নিতে হবে সেটা কিন্তু পৃথিবীতে বসে বিজ্ঞানীরা আগেভাগেই হিসেব কষে বের করে ফেলেছিলেন। জানো কি এরকম গতিশীল বস্তুর গতিপথ কিভাবে হিসেব করতে হয়?

ছবিঃ ১ 

প্রথমেই আমরা মহাকাশযানের গতিপথটাকে একটা কো-অর্ডিনেট সিস্টেমের মাধ্যমে প্রকাশ করবো। প্রথমে মহাকাশযানটির গতিপথ বরাবর একটি অক্ষরেখা আকলাম (মনেকরো সেটা হচ্ছে x-অক্ষ), আর সেটি যেখান থেকে যাত্রা শুরু করেছে সেই বিন্দুটিকে ধরে নিলাম ওই অক্ষরেখার কেন্দ্রবিন্দু । এবার অক্ষরেখা থেকে প্রতি এক কিলোমিটার দূরত্ব পর পর ছোট ছোট দাগ দিয়ে আলাদা করলাম। কোন কিছুর অবস্থান হিসেব করার এই পদ্ধতিকে জ্যামিতির ভাষায় বলা হয় কো-অর্ডিনেট সিস্টেমCoordinate system is a method for determining the position of something.।

ভেক্টর রাশি পরিচিতি

ধরো পৃথিবীর বায়ুমন্ডল ছেড়ে ৪০০ কিমি যাওয়ার পর ৪০ ডিগ্রি বাঁক নিয়ে ৩০০ কিমি গেলে। তারপর ৩০ ডিগ্রি বাঁক নিয়ে আরও ৪০০ কিমি গেলে, এভাবে কিছুদূর চলতে চলতে দিক পরিবর্তন করে একসময়ে গন্তব্যে পৌছালে। এখন একটি নির্দিষ্ট দিকে মহাকাশযানটি যতটুকু অতিক্রম করলো সেটিকে আমরা প্রকাশ করবো ভেক্টর রাশির সাহয্যে। যখন কোন বস্তু ছুটতে থাকে, তার একটা দিক থাকে; যখন কোন বস্তু ঘুড়তে থাকে তার একটা দিক থাকে; এমনকি যখন কোন বস্তুতে ধরে টানাহ্যাঁচড়া করা হয়, তারও একটা দিক থাকে। পদার্থবিজ্ঞানের ভাষায়, এদেরকে বলা হয় ভেক্টর রাশিA quantity with both direction and magnitude, such as displacement or velocity, is called a vector.।

এবং এই ভেক্টররাশিগুলি হিসেব করার জন্য অক্ষরেখার উপর একক দূরত্বে যে ছোট ছোট দাগ কেটেছি, সেগুলির সাহায্য নিবো। গাণিতিক পরিভাষায় এদেরকে বলা হয় একক ভেক্টর A unit vector is a vector of length 1, sometimes also called a direction vector. ।

ভেক্টর স্পেস

মনেকরো মহাকাশযানটি যেদিকে যতটুকু যাচ্ছে সেদিকটিকে গ্রাফ পেপারে একটা তীর চিহ্ন দিয়ে দেখালাম। মহাকাশযানটি যদি এদিক ওদিক ঘুরে যায়, তীর চিহ্নটিকেও আমরা সেদিকে ঘুরিয়ে দিবো। যদি কোন একদিকে মহাকাশযানটি অনেক্ষন ধরে চলে, তাহলে তীর চিহ্নের দৈর্ঘ্য বড় হবে, আর যদি অল্পক্ষন চলে তাহলে তীর চিহ্নের দৈর্ঘ্য কম হবে। তাহলে উদাহরন অনুযায়ী ৪০০ কিমি পর ৪০ ডিগ্রি বাঁক নিয়ে ৩০০ কিমি গেলে সেটাকে ছবিঃ ৩ এর মত করে আঁকা যাবে

ছবিঃ ৩ 

এবং এখানে $\vec{AB}$ একটি ভেক্টর, যার মান ৪০০ কিমি; $\vec{BC}$ আরেকটি ভেক্টর, যার মান ৩০০ কিমি। এখানে মহাকাশযানটিকে ৪০ ডিগ্রি কোণে ঘুরানোর অর্থ হচ্ছে $\vec{BC}$ ভেক্টরটি x-অক্ষের সাথে ৪০ ডিগ্রি কোণ তৈরি করে । ভেক্টরের ক্ষেত্রে কতক্ষন পর কতটুকু কোন দিকে ঘুরেছে, তা অত্যন্ত গুরুত্বপূর্ণ। এজন্য ভেক্টর রাশির যোগ, বিয়োগ, গুণ ইত্যাদির নিয়ম একটু আলাদা।

এভাবে এদিকে পৃথিবী থেকে মঙ্গলগ্রহে পৌছাতে মহাকাশযানটিকে কিছুদূর পরপর যতবার দিক পরিবর্তন করতে হয়েছে, সেটাকে বলা হয় ভেক্টর স্পেস ভেক্টর স্পেসকে সাধারণত V দিয়ে নির্দেশ করা হয়ে থাকে। ।

ভেক্টর উপাংশ

হিসাবের সুবিধার জন্য যেকোন ভেক্টরকে কো-অর্ডিনেটের অক্ষ বরাবর ভিন্ন ভিন্ন অংশে ভাগ করে ফেলা যায়। যেমন $\vec{BC}$ ভেক্টরটার কথাই ধরো, এটি x-অক্ষের সাথে ৪০ ডিগ্রি কোণ তৈরি করেছে। যেহেতু এখানে শুধুই x-y কো-অর্ডিনেট নিয়ে কাজ করছি, সেহেতু $\vec{BC}$ কে আমরা x ও y অক্ষ বরাবর দুইভাগে ভাগ করতে পারি । এদেরকে বলবো ওই ভেক্টরের উপাংশ ইংরেজিতে বলে vector component। দুইমাত্রিক কো-অর্ডিনেট সিস্টেমে ভেক্টরের উপাংশ দুইটি। তিনমাত্রিক কো-অর্ডিনেটে উপাংশ হবে তিনটি। ।

ভেক্টর উপাংশ কিভাবে হিসেব করবো?

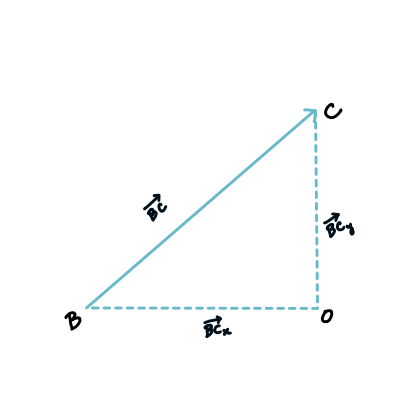ছবিঃ ৪ 

উপাংশ হিসেব করার জন্য $\vec{BC}$ এর B বিন্দু হতে x-অক্ষের সমান্তরাল আর C বিন্দু হতে y-অক্ষের সমান্তরাল দুইটি রেখা আঁকলাম। মনেকরো রেখা দুইটি O বিন্দুতে ছেদ করেছে। তাহলে BO হচ্ছে $\vec{BC}$ এর x-উপাংশ (একে লেখবো $\vec{BC}_x$ দিয়ে) আর CO হচ্ছে $\vec{BC}$ এর y-উপাংশ (একে লেখবো $\vec{BC}_y$ দিয়ে)।

এখানে আমরা পাচ্ছি একটা ত্রিভুজ $\Delta BOC$; যেনতেন ত্রিভুজ নয়, একটি সমকোণী ত্রিভুজ, যার $\angle BOC$ হচ্ছে ৯০ ডিগ্রি আর $\angle COB$ এর মান আমরা আগে থেকেই জানি, ৪০ ডিগ্রি। সুতরাং, ত্রিকোণমিত্রির সূত্র ব্যবহার করে আমরা পাচ্ছি- \begin{align} \cos\theta &= \dfrac{BC_x}{BC}\\ \Rightarrow BC_x &= BC\cos\theta \end{align} যেহেতু $\vec{BC}$ এর দৈর্ঘ্য আর $\angle COB$ এর মান আমরা জানি, এখান থেকে খুব সহজেই $BC_x$ এর মান বের করে ফেলতে পারবে। একইভাবে $BC_y$ এর জন্য লিখতে পারো- \begin{align} \sin\theta &= \dfrac{BC_y}{BC}\\ \Rightarrow BC_y &= BC \sin\theta \end{align} আবার, যেহেতু $\Delta BOC$ সমকোণী ত্রিভুজ, সেহেতু তুমি চাইলেই এখানে পিথাগোরাসের থিওরেম ব্যবহার করতে পারো। এখানে $BC$ হচ্ছে অতিভুজ, $BC_x$ লম্ব এবং $BC_y$ ভূমি। সুতরাং পিথাগোরাসের থিওরেম অনুসারে- \begin{align} BC=\sqrt{{BC_x}^2+{BC_y}^2} \end{align} অর্থাৎ যদি তুমি $BC_x$ আর $BC_y$ এর মান জানো তাহলে পিথাগোরাসের থিওরেম ব্যবহার করেই $BC$ এর মান বের করে ফেলতে পারবে। আবার \begin{align} \tan\theta &= \dfrac{BC_y}{BC_x}\\ \Rightarrow &= \tan^{-1}\dfrac{BC_y}{BC_x} \end{align} সমীকরণ দিয়ে $\vec{BC}$ কত ডিগ্রি কোণ তৈরি করেছে সেটা হিসেব করতে পারবে।

লক্ষ্য করোঃ এখানে সমীকরণ ১-৭ এ $\vec{BC}$, $\vec{BC_x}$ বা $\vec{BC_y}$ লেখার সময় ভেক্টর চিহ্ন ব্যবহার করিনি। কারণ এখানে শুধু ভেক্টর রাশিগুলির মান বসানো হয়েছে। ভেক্টর রাশির মান লেখার সময় এভাবে উপরের $\vec{arrow}$ ছাড়া (যেমনঃ $BC$) অথবা দুইটি লম্বা দাগের মধ্যে (যেমনঃ $|\vec{BC}|$) ভেক্টরটিকে বসিয়ে মান প্রকাশ করা হয়।

পরের পরিচ্ছেদ